XXTEA一个微型加密算法

对于的密码学算法来说，还是普遍使用对称密码学来实现对于文件或者数据的加密任务。其中主流的算法包括最为流行的 AES 分组密码算法，或者是常常用于移动设备中的 chacha20 序列密码。这些算法往往都各有优缺点。XXTEA 算法就是一种对称的分组加密算法，他的安全性欠缺，但是由于其结构和实现的简单性使得其称为了可以用于存储和计算能力欠缺的嵌入式设备之中，给这些设备提供最基本的密码学服务的算法。

XXTEA 是由 Roger Needham 和 David Wheeler 设计的，可以算作 TEA（Tiny Encryption Algorithm） 算法的第三代，在安全性上有所提升，同时效率提高。由于其代码实现非常简单，运算也是由异或等基本操作组成的，因此非常适合计算和存储能力吃紧的设备中使用。下面也可以看到其代码是非常简单的，寥寥几行无序复杂的运算就可以实现完整的加解密过程。

但是简洁也不是没有代价的，其安全性非常弱。2010 年 E. Yarrkov 证明其遭受基于选择明文的差分攻击，XXTEA 算法无法达到其秘钥空间的 128 bit 的安全，在约 2^59 次选择明文查询后，将可能恢复出秘钥。

XXTEA 算法的基本特点

• 没有分组加密模式的概念
• 没有初始向量 IV 的概念
• 分组长度可变，是任意 32 bit 为步长递增，最少 64 bit 的二进制字符串。
• 秘钥长度为 128 bit
• 加密轮数可变，取决于分组长度，分组越长轮数越少（最低6轮），分组短轮数越多（最多32个完整轮数）
• 没有置换表的概念，唯一常数是 DELTA=0x9e3779b9 ，可以作为算法逆向的判断依据

正是由于其轮数可变，当轮数较低的时候，提供了攻击的可能性。此外，分组加密方式、IV等的缺失，导致了其不可能作为一个大批量数据的手段，仅用于安全需求低、消息较短的嵌入式或者web等较弱环境下。但是也有一些优点：

• 具有良好雪崩效应
• 正确使用（明文添加序列号），则可以尽可能避免缺少IV带来的构建 identity message 攻击
• 良好的抗切割和合并攻击

其基本结构如下：

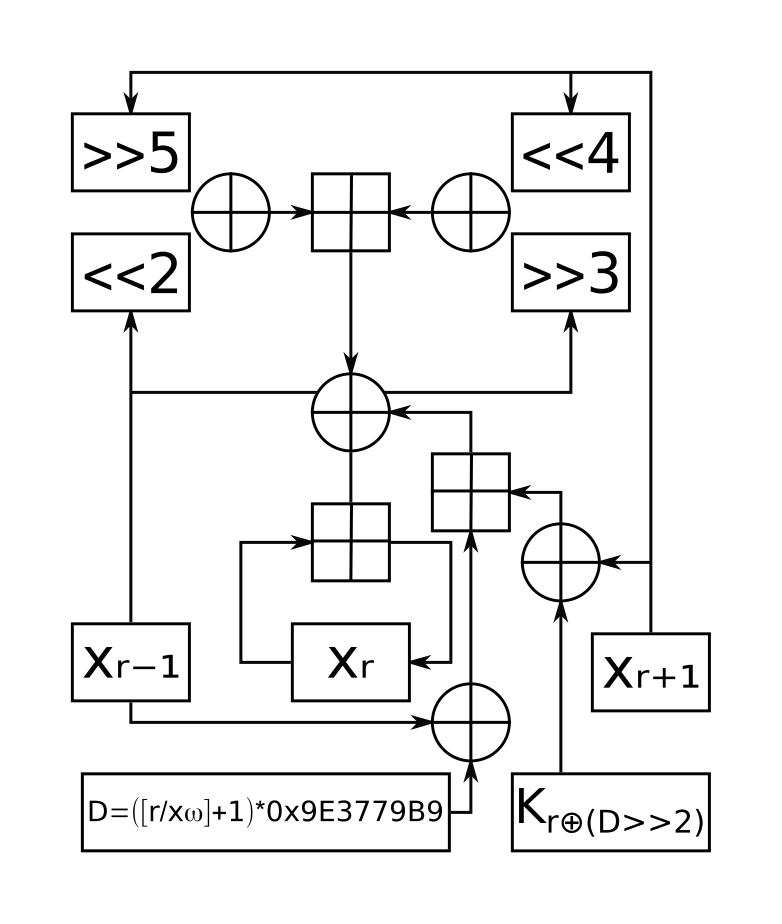
算法实现如下（参加 wikipidea）

#define MX ((z>>5^y<<2) + (y>>3^z<<4) ^ (sum^y) + (k[p&3^e]^z))
  
long btea(long* v, long n, long* k) {
    unsigned long z=v[n-1], y=v[0], sum=0, e, DELTA=0x9e3779b9;
    long p, q ;
    if (n > 1) {          /* Coding Part */
        q = 6 + 52/n;
        while (q-- > 0) {
            sum += DELTA;
            e = (sum >> 2) & 3;
            for (p=0; p<n-1; p++) y = v[p+1], z = v[p] += MX;
            y = v[0];
            z = v[n-1] += MX;
        }
        return 0 ; 
    } else if (n < -1) {  /* Decoding Part */
    n = -n;
    q = 6 + 52/n;
    sum = q*DELTA ;
    while (sum != 0) {
        e = (sum >> 2) & 3;
        for (p=n-1; p>0; p--) z = v[p-1], y = v[p] -= MX;
        z = v[n-1];
        y = v[0] -= MX;
        sum -= DELTA;
    }
    return 0;
  }
  return 1;
}

变种和应用

QQ 曾经使用的就是 TEA（可能非XXTEA） 算法的固定 16 轮分组加密变种。